Analysis Toolpak Add-in For Mac
Posted By admin On 21.02.20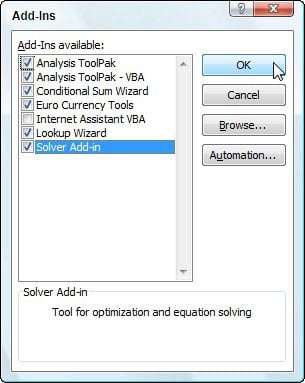
Excel for Office 365 Excel for Office 365 for Mac Excel 2019 Excel 2016 Excel 2019 for Mac Excel 2013 Excel 2010 Excel 2007 Excel 2016 for Mac If you need to develop complex statistical or engineering analyses, you can save steps and time by using the Analysis ToolPak. You provide the data and parameters for each analysis, and the tool uses the appropriate statistical or engineering macro functions to calculate and display the results in an output table. Some tools generate charts in addition to output tables. The data analysis functions can be used on only one worksheet at a time. When you perform data analysis on grouped worksheets, results will appear on the first worksheet and empty formatted tables will appear on the remaining worksheets. To perform data analysis on the remainder of the worksheets, recalculate the analysis tool for each worksheet.
The Analysis ToolPak includes the tools described in the following sections. To access these tools, click Data Analysis in the Analysis group on the Data tab. If the Data Analysis command is not available, you need to load the Analysis ToolPak add-in program. Click the File tab, click Options, and then click the Add-Ins category.
If you're using Excel 2007, click the Microsoft Office Button, and then click Excel Options. In the Manage box, select Excel Add-ins and then click Go. If you're using Excel for Mac, in the file menu go to Tools Excel Add-ins. In the Add-Ins box, check the Analysis ToolPak check box, and then click OK. If Analysis ToolPak is not listed in the Add-Ins available box, click Browse to locate it. If you are prompted that the Analysis ToolPak is not currently installed on your computer, click Yes to install it.
The CORREL and PEARSON worksheet functions both calculate the correlation coefficient between two measurement variables when measurements on each variable are observed for each of N subjects. (Any missing observation for any subject causes that subject to be ignored in the analysis.) The Correlation analysis tool is particularly useful when there are more than two measurement variables for each of N subjects.
Zoom search engine keygen for mac. It provides an output table, a correlation matrix, that shows the value of CORREL (or PEARSON) applied to each possible pair of measurement variables. The correlation coefficient, like the covariance, is a measure of the extent to which two measurement variables 'vary together.' Unlike the covariance, the correlation coefficient is scaled so that its value is independent of the units in which the two measurement variables are expressed. (For example, if the two measurement variables are weight and height, the value of the correlation coefficient is unchanged if weight is converted from pounds to kilograms.) The value of any correlation coefficient must be between -1 and +1 inclusive.
Excel Analysis Toolpak Office 365
You can use the correlation analysis tool to examine each pair of measurement variables to determine whether the two measurement variables tend to move together — that is, whether large values of one variable tend to be associated with large values of the other (positive correlation), whether small values of one variable tend to be associated with large values of the other (negative correlation), or whether values of both variables tend to be unrelated (correlation near 0 (zero)). The Correlation and Covariance tools can both be used in the same setting, when you have N different measurement variables observed on a set of individuals.
The Correlation and Covariance tools each give an output table, a matrix, that shows the correlation coefficient or covariance, respectively, between each pair of measurement variables. The difference is that correlation coefficients are scaled to lie between -1 and +1 inclusive. Corresponding covariances are not scaled. Both the correlation coefficient and the covariance are measures of the extent to which two variables 'vary together.' The Covariance tool computes the value of the worksheet function COVARIANCE.P for each pair of measurement variables.
(Direct use of COVARIANCE.P rather than the Covariance tool is a reasonable alternative when there are only two measurement variables, that is, N=2.) The entry on the diagonal of the Covariance tool's output table in row i, column i is the covariance of the i-th measurement variable with itself. This is just the population variance for that variable, as calculated by the worksheet function VAR. You can use the Covariance tool to examine each pair of measurement variables to determine whether the two measurement variables tend to move together — that is, whether large values of one variable tend to be associated with large values of the other (positive covariance), whether small values of one variable tend to be associated with large values of the other (negative covariance), or whether values of both variables tend to be unrelated (covariance near 0 (zero)).
The F-Test Two-Sample for Variances analysis tool performs a two-sample F-test to compare two population variances. For example, you can use the F-Test tool on samples of times in a swim meet for each of two teams. The tool provides the result of a test of the null hypothesis that these two samples come from distributions with equal variances, against the alternative that the variances are not equal in the underlying distributions. The tool calculates the value f of an F-statistic (or F-ratio). A value of f close to 1 provides evidence that the underlying population variances are equal. In the output table, if f 1, 'P(F. The Moving Average analysis tool projects values in the forecast period, based on the average value of the variable over a specific number of preceding periods.
A moving average provides trend information that a simple average of all historical data would mask. Use this tool to forecast sales, inventory, or other trends.
Each forecast value is based on the following formula. Where:.
N is the number of prior periods to include in the moving average. A j is the actual value at time j.
F j is the forecasted value at time j. The Regression analysis tool performs linear regression analysis by using the 'least squares' method to fit a line through a set of observations.
You can analyze how a single dependent variable is affected by the values of one or more independent variables. For example, you can analyze how an athlete's performance is affected by such factors as age, height, and weight. You can apportion shares in the performance measure to each of these three factors, based on a set of performance data, and then use the results to predict the performance of a new, untested athlete.
The Regression tool uses the worksheet function LINEST. The Sampling analysis tool creates a sample from a population by treating the input range as a population. When the population is too large to process or chart, you can use a representative sample. You can also create a sample that contains only the values from a particular part of a cycle if you believe that the input data is periodic. For example, if the input range contains quarterly sales figures, sampling with a periodic rate of four places the values from the same quarter in the output range. The Two-Sample t-Test analysis tools test for equality of the population means that underlie each sample. The three tools employ different assumptions: that the population variances are equal, that the population variances are not equal, and that the two samples represent before-treatment and after-treatment observations on the same subjects.
For all three tools below, a t-Statistic value, t, is computed and shown as 't Stat' in the output tables. Depending on the data, this value, t, can be negative or nonnegative. Under the assumption of equal underlying population means, if t =0, 'P(T. Note: Among the results that are generated by this tool is pooled variance, an accumulated measure of the spread of data about the mean, which is derived from the following formula.
T-Test: Two-Sample Assuming Equal Variances This analysis tool performs a two-sample student's t-Test. This t-Test form assumes that the two data sets came from distributions with the same variances. It is referred to as a homoscedastic t-Test. You can use this t-Test to determine whether the two samples are likely to have come from distributions with equal population means. T-Test: Two-Sample Assuming Unequal Variances This analysis tool performs a two-sample student's t-Test.
This t-Test form assumes that the two data sets came from distributions with unequal variances. It is referred to as a heteroscedastic t-Test. As with the preceding Equal Variances case, you can use this t-Test to determine whether the two samples are likely to have come from distributions with equal population means.
Use this test when there are distinct subjects in the two samples. Use the Paired test, described in the follow example, when there is a single set of subjects and the two samples represent measurements for each subject before and after a treatment. The following formula is used to determine the statistic value t. The following formula is used to calculate the degrees of freedom, df. Because the result of the calculation is usually not an integer, the value of df is rounded to the nearest integer to obtain a critical value from the t table. The Excel worksheet function T. TEST uses the calculated df value without rounding, because it is possible to compute a value for T.
TEST with a noninteger df. Because of these different approaches to determining the degrees of freedom, the results of T. TEST and this t-Test tool will differ in the Unequal Variances case. The z-Test: Two Sample for Means analysis tool performs a two sample z-Test for means with known variances. This tool is used to test the null hypothesis that there is no difference between two population means against either one-sided or two-sided alternative hypotheses.
If variances are not known, the worksheet function Z. TEST should be used instead. When you use the z-Test tool, be careful to understand the output. 'P(Z = ABS(z)), the probability of a z-value further from 0 in the same direction as the observed z value when there is no difference between the population means. 'P(Z = ABS(z) or Z.